Wilcoxon Signed-Rank Test using SPSS Statistics
Introduction
The Wilcoxon signed-rank test is the nonparametric test equivalent to the dependent t-test. As the Wilcoxon signed-rank test does not assume normality in the data, it can be used when this assumption has been violated and the use of the dependent t-test is inappropriate. It is used to compare two sets of scores that come from the same participants. This can occur when we wish to investigate any change in scores from one time point to another, or when individuals are subjected to more than one condition.
For example, you could use a Wilcoxon signed-rank test to understand whether there was a difference in smokers' daily cigarette consumption before and after a 6 week hypnotherapy programme (i.e., your dependent variable would be "daily cigarette consumption", and your two related groups would be the cigarette consumption values "before" and "after" the hypnotherapy programme). You could also use a Wilcoxon signed-rank test to understand whether there was a difference in reaction times under two different lighting conditions (i.e., your dependent variable would be "reaction time", measured in milliseconds, and your two related groups would be reaction times in a room using "blue light" versus "red light").
This "quick start" guide shows you how to carry out a Wilcoxon signed-rank test using SPSS Statistics, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a Wilcoxon signed-rank test to give you a valid result. We discuss these assumptions next.
SPSS Statistics
top ^
Assumptions
When you choose to analyse your data using a Wilcoxon signed-rank test, part of the process involves checking to make sure that the data you want to analyse can actually be analysed using a Wilcoxon signed-rank test. You need to do this because it is only appropriate to use a Wilcoxon signed-rank test if your data "passes" three assumptions that are required for a Wilcoxon signed-rank test to give you a valid result. The first two assumptions relate to your study design and the types of variables you measured. The third assumption reflects the nature of your data and is the one assumption you test using SPSS Statistics. These three assumptions as briefly explained below:
- Assumption #1: Your dependent variable should be measured at the ordinal or continuous level. Examples of ordinal variablesinclude Likert scales (e.g., a 7-point scale from "strongly agree" through to "strongly disagree"), amongst other ways of ranking categories (e.g., a 5-point scale explaining how much a customer liked a product, ranging from "Not very much" to "Yes, a lot"). Examples of continuous variables (i.e., interval or ratio variables) include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth. You can learn more about ordinal and continuous variables in our article: Types of Variable.
- Assumption #2: Your independent variable should consist of two categorical, "related groups" or "matched pairs". "Related groups" indicates that the same subjects are present in both groups. The reason that it is possible to have the same subjects in each group is because each subject has been measured on two occasions on the same dependent variable. For example, you might have measured 10 individuals' performance in a spelling test (the dependent variable) before and after they underwent a new form of computerized teaching method to improve spelling. You would like to know if the computer training improved their spelling performance. The first related group consists of the subjects at the beginning (prior to) the computerized spelling training and the second related group consists of the same subjects, but now at the end of the computerized training. The Wilcoxon signed-rank test can also be used to compare different subjects within a "matched-pairs" study design, but this does not happen very often. Nonetheless, to learn more about the different study designs you use with a Wilcoxon signed-rank test, see our enhanced Wilcoxon signed-rank test guide.
- Assumption #3: The distribution of the differences between the two related groups (i.e., the distribution of differences between the scores of both groups of the independent variable; for example, the reaction time in a room with "blue lighting" and a room with "red lighting") needs to be symmetrical in shape. If the distribution of differences is symmetrically shaped, you can analyse your study using the Wilcoxon signed-rank test. In practice, checking for this assumption just adds a little bit more time to your analysis, requiring you to click a few more buttons in SPSS Statistics when performing your analysis, as well as think a little bit more about your data, but it is not a difficult task. However, do not be surprised if, when analysing your own data using SPSS Statistics, this assumption is violated (i.e., is not met). This is not uncommon when working with real-world data rather than textbook examples, which often only show you how to carry out a Wilcoxon signed-rank test when everything goes well! However, even when your data fails this assumption, there is often a solution to overcome this, such as transforming your data to achieve a symmetrically-shaped distribution of differences (not a preferred option) or running a sign test instead of the Wilcoxon signed-rank test. If you are unsure of the procedures in SPSS Statistics to test this assumption or how to interpret the SPSS Statistics output, we show you how in our enhanced Wilcoxon signed-rank test guide, which you can access by subscribing to the site here.
In the section, Test Procedure in SPSS Statistics, we illustrate the SPSS Statistics procedure to perform a Wilcoxon signed-rank test. First, we introduce the example that is used in this "quick start" guide.
SPSS Statistics
top ^
Example
A pain researcher is interested in finding methods to reduce lower back pain in individuals without having to use drugs. The researcher thinks that having acupuncture in the lower back might reduce back pain. To investigate this, the researcher recruits 25 participants to their study. At the beginning of the study, the researcher asks the participants to rate their back pain on a scale of 1 to 10, with 10 indicating the greatest level of pain. After 4 weeks of twice weekly acupuncture, the participants are asked again to indicate their level of back pain on a scale of 1 to 10, with 10 indicating the greatest level of pain. The researcher wishes to understand whether the participants' pain levels changed after they had undergone the acupuncture, so a Wilcoxon signed-rank test is run.
In our enhanced Wilcoxon signed-rank test guide, we show you how to correctly enter data in SPSS Statistics to run a Wilcoxon signed-rank test. You can learn about our enhanced data setup content here. Alternately, we have a generic, "quick start" guide to show you how to enter data into SPSS Statistics, available here. In our enhanced Wilcoxon signed-rank test guide, we also explain how to deal with missing values in your data set (e.g., if a participant completed a pre-test, but failed to turn up to the post-test). In the next section, we take you through the Wilcoxon signed-rank test procedure using SPSS Statistics.
Wilcoxon signed-rank test
From Wikipedia, the free encyclopedia
The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used when comparing two related samples, matched samples, or repeated measurements on a single sample to assess whether their population mean ranks differ (i.e. it is a paired difference test). It can be used as an alternative to the paired Student's t-test, t-test for matched pairs, or the t-test for dependent samples when the population cannot be assumed to be normally distributed.[1]
The Wilcoxon signed-rank test is not the same as the Wilcoxon rank-sum test, although both are nonparametric and involve summation of ranks.
Contents
[hide]History[edit]
The test is named for Frank Wilcoxon (1892–1965) who, in a single paper, proposed both it and the rank-sum test for two independent samples (Wilcoxon, 1945).[2] The test was popularized by Sidney Siegel (1956) in his influential text book on non-parametric statistics.[3] Siegel used the symbol T for a value related to, but not the same as,  . In consequence, the test is sometimes referred to as the Wilcoxon T test, and the test statistic is reported as a value of T.
. In consequence, the test is sometimes referred to as the Wilcoxon T test, and the test statistic is reported as a value of T.
 . In consequence, the test is sometimes referred to as the Wilcoxon T test, and the test statistic is reported as a value of T.
. In consequence, the test is sometimes referred to as the Wilcoxon T test, and the test statistic is reported as a value of T.Assumptions[edit]
- Data are paired and come from the same population.
- Each pair is chosen randomly and independently.
- The data are measured at least on an ordinal scale (cannot be nominal).
Test procedure[edit]
Let  be the sample size, the number of pairs. Thus, there are a total of 2N data points. For
be the sample size, the number of pairs. Thus, there are a total of 2N data points. For  , let
, let 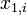 and
and  denote the measurements.
denote the measurements.
 be the sample size, the number of pairs. Thus, there are a total of 2N data points. For
be the sample size, the number of pairs. Thus, there are a total of 2N data points. For  , let
, let 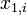 and
and  denote the measurements.
denote the measurements.- H0: difference between the pairs follows a symmetric distribution around zero
- H1: difference between the pairs does not follow a symmetric distribution around zero.
- For
 , calculate
, calculate  and
and 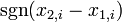 , where
, where 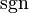 is the sign function.
is the sign function. - Exclude pairs with
 . Let
. Let  be the reduced sample size.
be the reduced sample size. - Order the remaining
 pairs from smallest absolute difference to largest absolute difference,
pairs from smallest absolute difference to largest absolute difference,  .
. - Rank the pairs, starting with the smallest as 1. Ties receive a rank equal to the average of the ranks they span. Let
 denote the rank.
denote the rank. -
![W = \sum_{i=1}^{N_r} [\sgn(x_{2,i} - x_{1,i}) \cdot R_i]](https://upload.wikimedia.org/math/5/8/1/581d1a83ad20dc5eb35f6b0f49ec0647.png) , the sum of the signed ranks.
, the sum of the signed ranks.
- Under null hypothesis,
 follows a specific distribution with no simple expression. This distribution has an expected value of 0 and a variance of
follows a specific distribution with no simple expression. This distribution has an expected value of 0 and a variance of  .
. can be compared to a critical value from a reference table.[1]
can be compared to a critical value from a reference table.[1]- The two-sided test consists in rejecting
 , if
, if 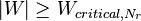 .
.
- As
 increases, the sampling distribution of
increases, the sampling distribution of  converges to a normal distribution. Thus,
converges to a normal distribution. Thus,
The T statistic used by Siegel is the smaller of two sums of ranks of given sign; in the example given below, therefore, T would equal 3+4+5+6=18. Low values of T are required for significance. As will be obvious from the example below, T is easier to calculate by hand than W and the test is equivalent to the two-sided test above-described (the distribution of the statistic under H0 has to be adjusted).
Excluding zeros is not a statistically justified method and such an approach can lead to enormous calculation errors. A more stable method is:[4]
- Calculate
![W = \sum_{i=1}^{N} [\sgn(x_{2,i} - x_{1,i}) \cdot R_i]](https://upload.wikimedia.org/math/1/a/6/1a6f29a396eab2cfefb454ade7b21d91.png) , (assume sgn(0) = 0)
, (assume sgn(0) = 0) - Calculate sampling probabilities

- For
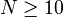 use normal approximation
use normal approximation 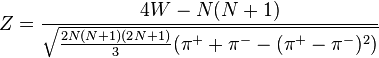 .
.
(Note that this value is undefined if either 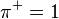 or
or  : i.e. if all samples show positive effect or all samples show negative effect. This is not the case with the test statistic as originally defined.)
: i.e. if all samples show positive effect or all samples show negative effect. This is not the case with the test statistic as originally defined.)
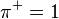 or
or  : i.e. if all samples show positive effect or all samples show negative effect. This is not the case with the test statistic as originally defined.)
: i.e. if all samples show positive effect or all samples show negative effect. This is not the case with the test statistic as originally defined.)Example[edit]
| order by absolute difference |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 is the sign function,
is the sign function,  is the absolute value, and
is the absolute value, and  is the rank. Notice that pairs 3 and 9 are tied in absolute value. They would be ranked 1 and 2, so each gets the average of those ranks, 1.5.
is the rank. Notice that pairs 3 and 9 are tied in absolute value. They would be ranked 1 and 2, so each gets the average of those ranks, 1.5.
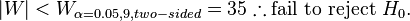
Effect size[edit]
To compute an effect size for the signed-rank test, one can use the rank correlation.
If the test statistic W is reported, Kerby (2014) has shown that the rank correlation r is equal to the test statistic W divided by the total rank sum S, or r = W/S.[5] Using the above example, the test statistic is W = 9. The sample size of 9 has a total rank sum of S = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 45. Hence, the rank correlation is 9/45, so r = .20.
If the test statistic T is reported, an equivalent way to compute the rank correlation is with the difference in proportion between the two rank sums, which is the Kerby (2014) simple difference formula.[5] To continue with the current example, the sample size is 9, so the total rank sum is 45. T is the smaller of the two rank sums, so T is 3 + 4 + 5 + 6 = 18. From this information alone, the remaining rank sum can be computed, because it is the total sum S minus T, or in this case 45 - 18 = 27. Next, the two rank-sum proportions are 27/45 = 60% and 18/45 = 40%. Finally, the rank correlation is the difference between the two proportions (.60 minus .40), hence r = .20.
See also[edit]
- Mann–Whitney–Wilcoxon test (the variant for two independent samples)
- Sign test (Like Wilcoxon test, but without the assumption of symmetric distribution of the differences around the median, and without using the magnitude of the difference)
References[edit]
- ^
- ^ Wilcoxon, Frank (Dec 1945). "Individual comparisons by ranking methods" (PDF). Biometrics Bulletin 1 (6): 80–83.
- ^ Siegel, Sidney (1956). Non-parametric statistics for the behavioral sciences. New York: McGraw-Hill. pp. 75–83.
- ^ Ikewelugo Cyprian Anaene Oyeka (Apr 2012). "Modified Wilcoxon Signed-Rank Test". Open Journal of Statistics: 172–176.
- ^a b Kerby, D. S. (2014). The simple difference formula: An approach to teaching nonparametric correlation. Innovative Teaching, volume 3, article 1. doi:10.2466/11.IT.3.1. link to pdf


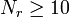 , a
, a 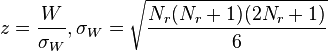 .
.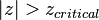 then reject
then reject 
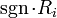
No comments :
Post a Comment
Note: only a member of this blog may post a comment.